 Home > Nature of light > The mysterious behavior of individual photons
Home > Nature of light > The mysterious behavior of individual photons
The mysterious behavior of individual photons

In 1807, Thomas Young confirmed that light shows properties of a wave through his interference experiment.
If light is a wave, then is it a “transverse wave” like a radio wave?
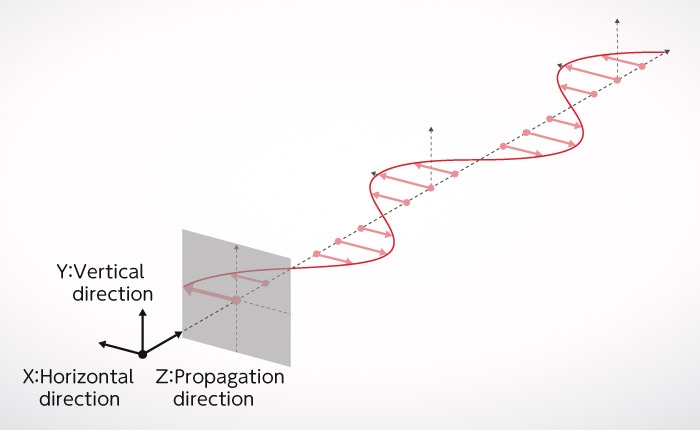
Or is it a “longitudinal wave” like sound?
Around the same time as Thomas Young, Augustin-Jean Fresnel and Domonique François Jean Arago found the answer to that question.
The concept of “polarized light”, which was known of since that time, was used in their experiment.
On this page we introduce their experiment using “polarized light”.
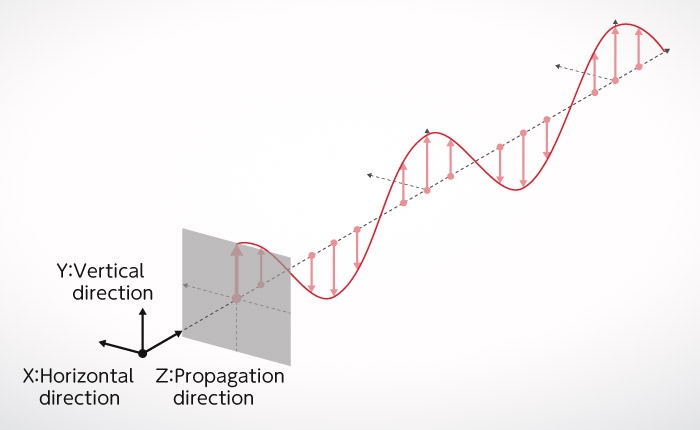
Light is a transverse wave
Young's interference experiment, introduced in Wave-Particle Duality of Photons, can explain how interference fringes occur even if light is a “longitudinal wave”. Fresnel and Arago conducted interference experiments using the concept of “polarized light”, which was already known of at the time, and they proved that light is a “transverse wave”. This revealed another aspect of the true form of light.
Understand polarized light in diagrams
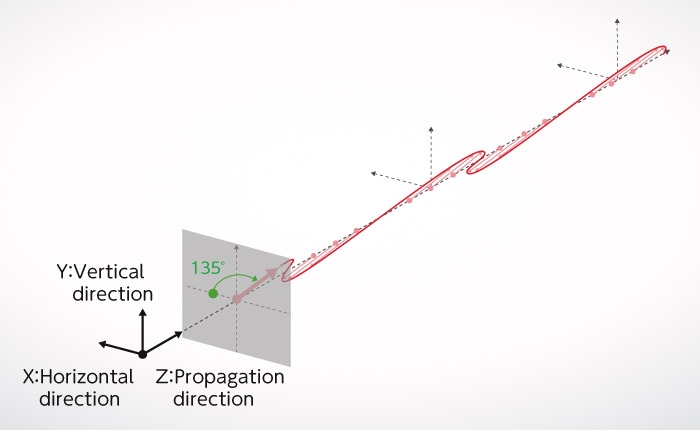
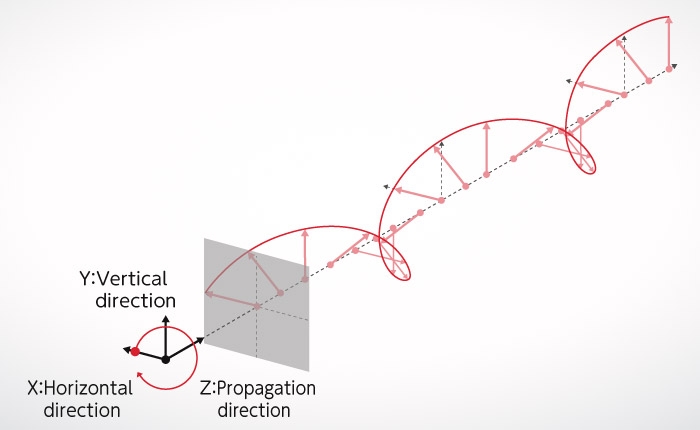
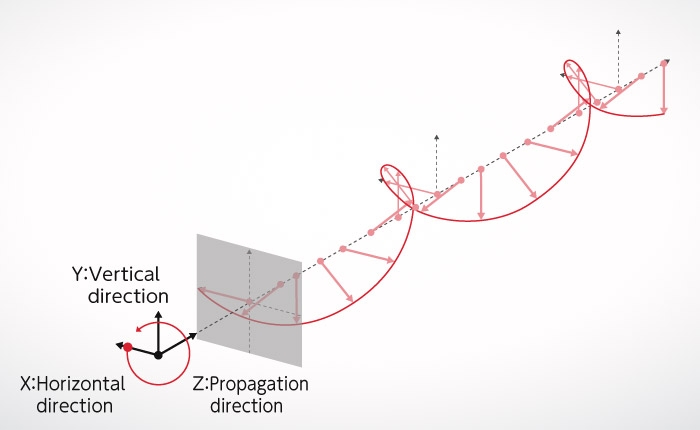
Fresnel / Arago Experiment
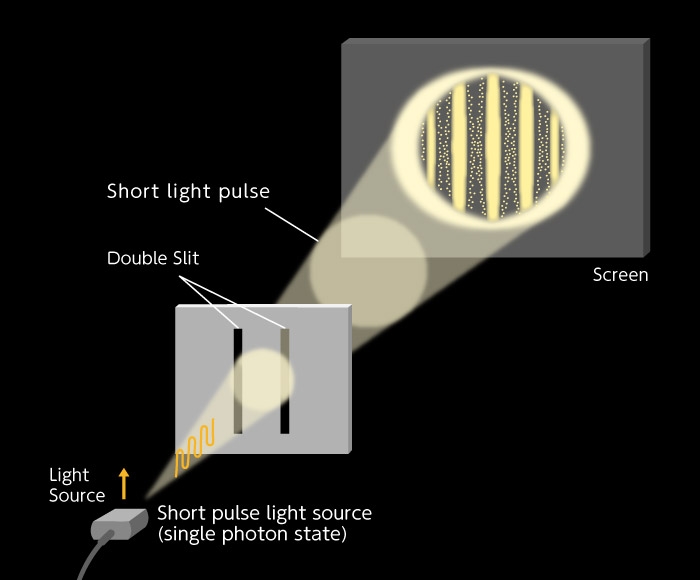
In Young's interference experiment with a single photon, which was introduced in Wave-Particle Duality of Photons, interference fringes showing the nature of waves appeared because of light transmitted through double slits. In this experiment, a single photon passed through both of the slits at the same time, despite the fact that it is thought to be just one particle, creating interference fringes that behaved like waves.
From these results, we can see that photons have the properties of both particles and waves, which is to say that they exhibit wave-particle duality.
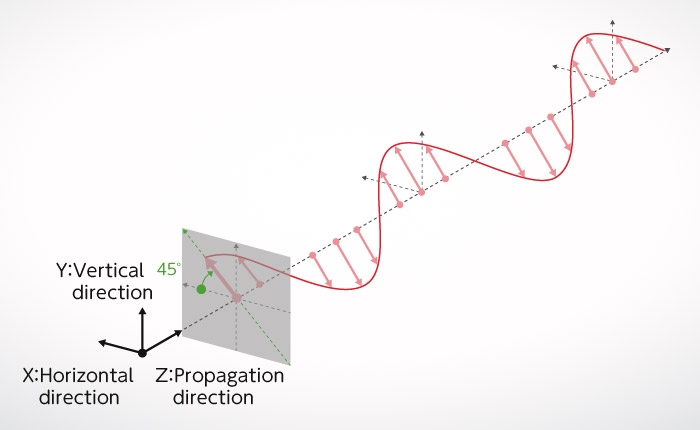
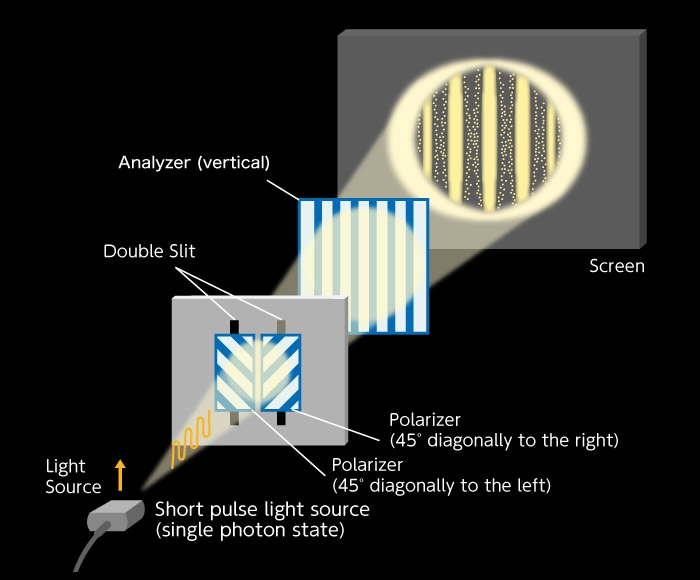
Next, look at the experimental set up of Fresnel and Arago in Figure B. Unlike Young's interference experiment, the double slits have a polarizer tilted 45° to the right and a polarizer tilted 45° to the left, respectively. For this reason, polarization of light, which is in fact “transverse waves” emerging from each slit, is an independent component positioned orthogonal to each other. The pink arrow and the green arrow in the figure indicate the directions of polarization. In Figure B-1, pink and green are orthogonal to each other. Here, no interference fringes appear on the screen (Figure B-1).
Reference: Nikkei Science March 2012 32 “Photon Paradox”
As a result, it is different from the results of Young's interference experiment, explained earlier in Wave-Particle Duality of Photons. It may be difficult to understand why interference fringes do not appear, but this will be explained later in another way.
Next, as shown in Figure B-2, a vertical analyzer is placed behind the double slit (this is the same as a polarizer, but when several polarizers are placed on the same optical path, the last one is called analyzer). Now what happens? The polarization (oscillation direction) of light emitted from the right slit is tilted at a 45° angle to the right, but when it passes through the analyzer, the oscillation direction changes to vertical. Similarly, the polarization of light emitted from the left slit also has a vertical oscillation direction. There, both lights are polarized vertically on the final screen, so interference fringes appear because of interference (Figure B-2).
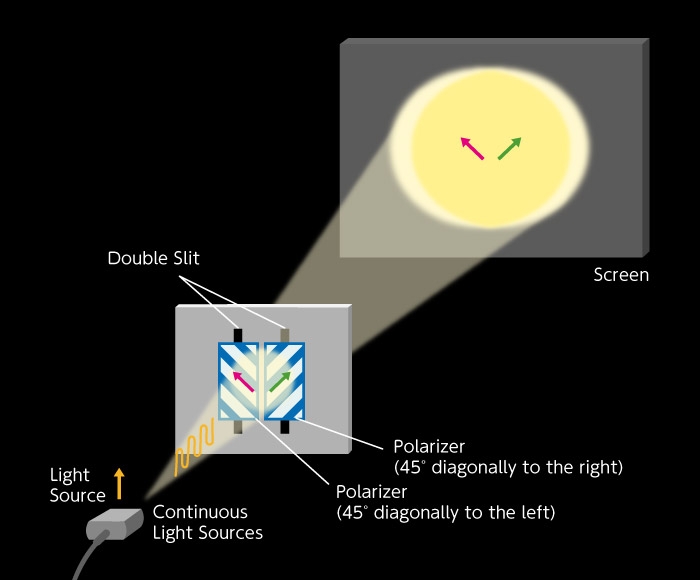
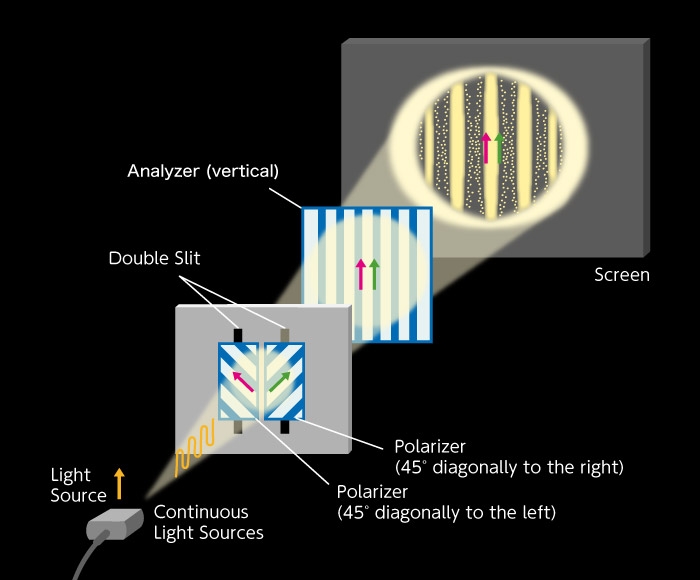
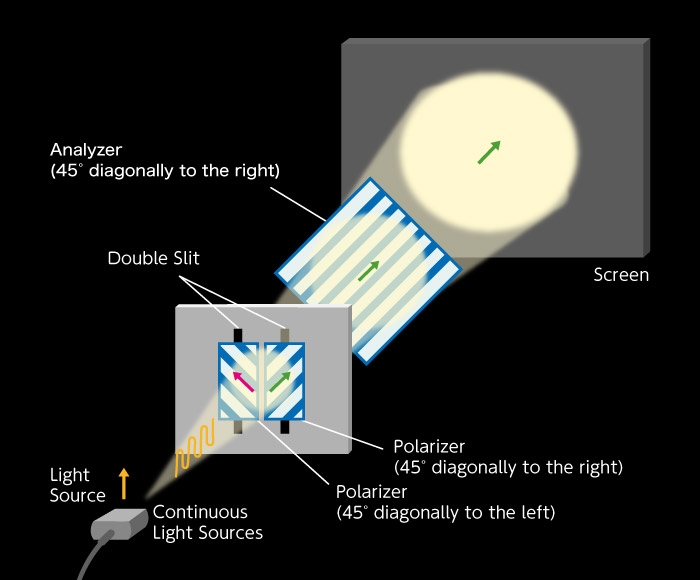
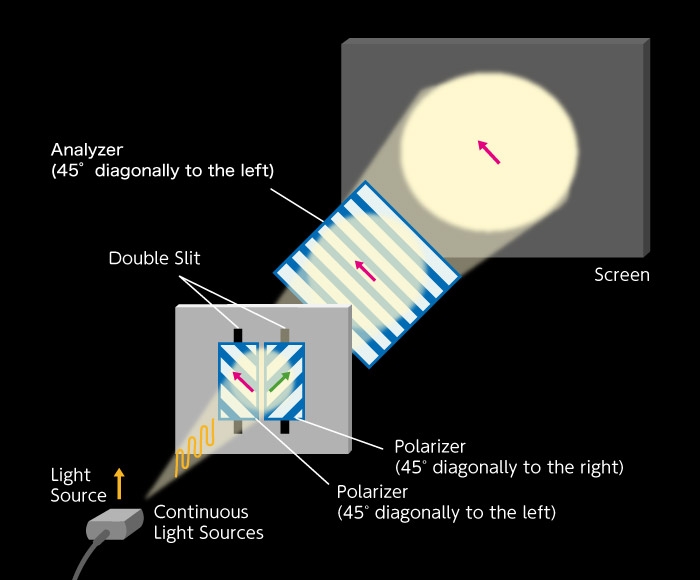
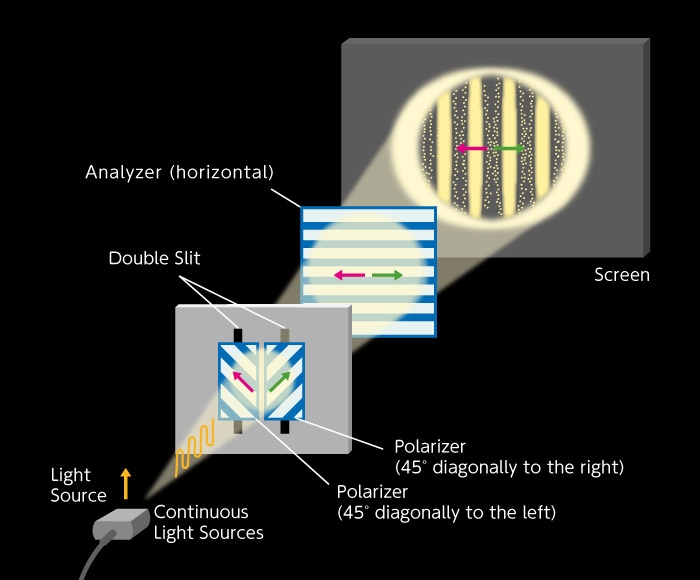
Finally, let's take look at Figure B-1, our first figure, and explain it in different terms. In this experiment, there is no analyzer. Following Figure B-2 and Figure B-5, we divide the two polarized “transverse waves” tilted 45° left and 45° right respectively, which passed through the double slits, so they are divided into four polarized lights; two vertically polarized lights and two horizontally polarized lights. The interference fringes that appear from the two vertically polarized lights as shown in Figure B-2 have bright centers. The interference fringes that appear the from two horizontally polarized lights as shown in Figure B-5 have dark centers. As such, the interference fringes have disappeared entirely as a result of overlap between the two interference fringes where bright and dark light have different positions. So, is it clear now?

Individual photons of short light pulses

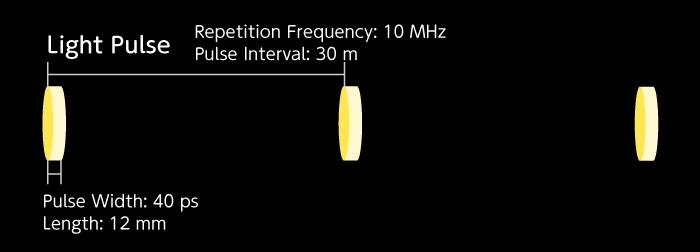
Experiments conducted by Hamamatsu Photonics
(Fresnel / Arago polarization interference experiment in a short pulse single photon state)
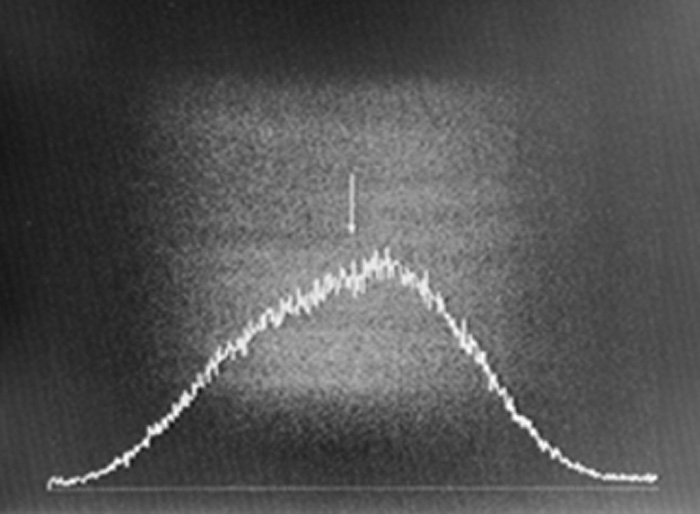
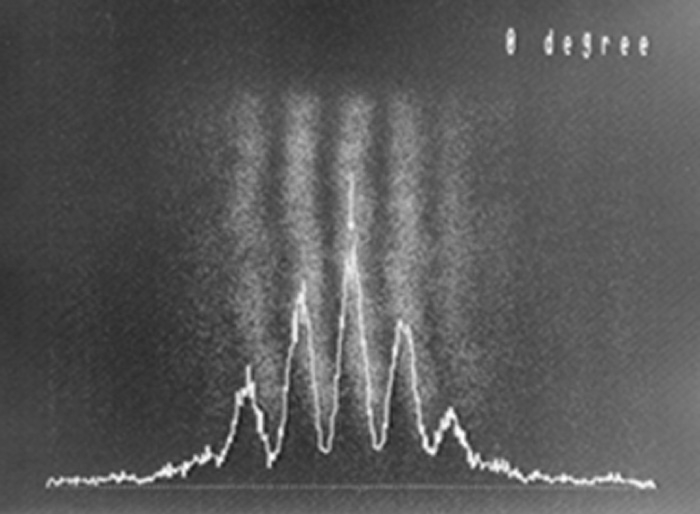
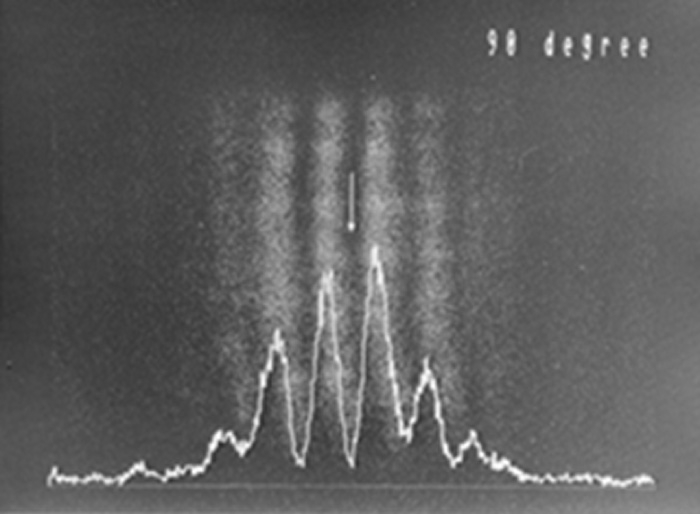
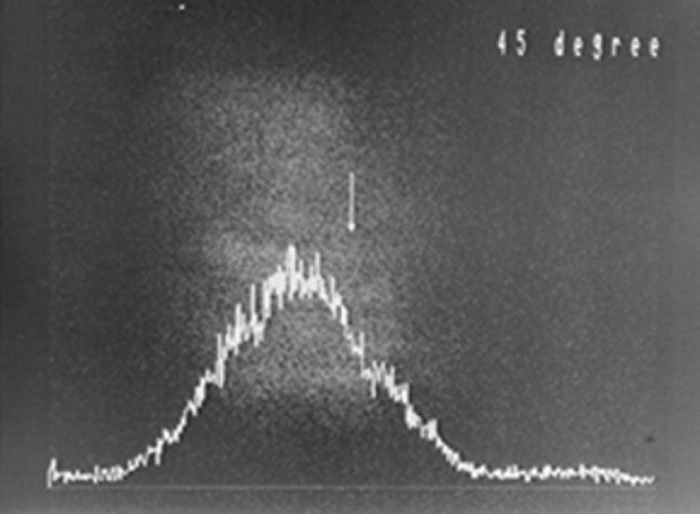
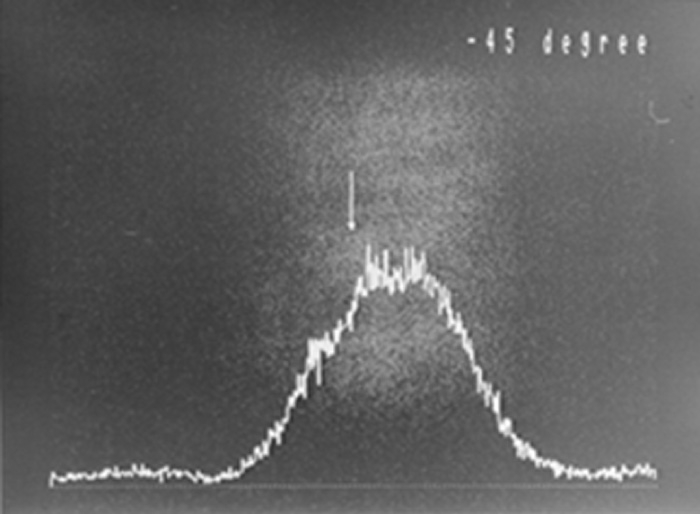
As we saw in Figure B-6, two polarized lights crossing at a right angle do not interfere with each other, so there are no interference fringes occur in Figure E-1. The light from both slits is observed, and appears to spread both left and right. In Figure E-2, interference fringes can be seen just like in Young's interference experiment (Video 2). In Figure E-3, dark and bright light positions are opposite of those in Figure E-2. In Figure E-4, only the light from the slit on the right is transmitted, so it is biased to the left (left and right appear inverted in cameras). In Figure E-5, the pattern is the opposite of Figure E-4. In the final experiment, the normal Fresnel / Arago polarization interference experiment was expanded upon to use circularly polarized light. Specifically, a quarter wavelength plate was added in front of the double slit. Results of this experiment are shown in Figure E-6. In this state, there is a quarter wavelength phase shift in the polarized light components that pass through each of the double slits. The phase shift moved the interference fringes laterally by a quarter wavelength, and the center of the screen is located in the midpoint of the bright and dark parts of the interference fringes.

Please refer to this page (Copyrights and trademarks) in order to use or quote the images and video content on this page for other media.
See these references on "Young's Interference Experiment with a Single Photon Using Short Light Pulses" and ”Fresnel / Arago polarization interference experiment in a short pulse single photon state”.
Reference (1)
H. Takahashi, S. Aoshima, T. Urakami, T. Takemori, I. Hirano, and Y. Tsuchiya, Young's Interference Experiment in the Single-Photon Region Using Short Optical Pulses, Kogaku, 20 (1991) 108-111. [published in Japanese]
https://annex.jsap.or.jp/photonics/kogaku/public/20-02-kenkyu6.pdf
Reference (2)
H. Takahashi, S. Aoshima, T. Urakami, T. Takemori, I. Hirano, and Y. Tsuchiya, Interference Experiment of Polarized Light in the Single-Photon Region, Kogaku, 21 (1992) 165-168. [published in Japanese]
https://annex.jsap.or.jp/photonics/kogaku/public/21-03-kenkyu.pdf
In this experiment, some things seem mysterious indeed. In Young's interference experiment, a single photon was observed passing through two slits at the same time and appearing as a particle on the screen, resulting in interference fringes that show its nature as a wave. In the Fresnel & Arago interference experiment, a polarized photon that has passed through the two slits appears as “transverse waves” 45˚ diagonal to the right and 45˚ diagonal to the left. Consider this: what are the implications of the fact that a single photon can show states of two perpendicular polarized lights at the same time? And what happens after it passes through the analyzer?
They discovered one of the true natures of light, which is that light is a “transverse wave”. Simultaneously, through more advanced experiments using “polarized light”, they found that a photon exhibits even more mysterious behavior. For all of us seeking to find the true nature of photons, this invites us to look ever deeper into the mysteries of light. In 1917, Albert Einstein said, “For the rest of my life, I will reflect on what light is.” Likewise, light continues to motivate us to take on new challenges.

Mr. TAKAHASHI







